
শ্রেণি – দশম | বিভাগ – গণিত | অধ্যায় – বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য (Theorems related to Tangent to a circle) | Britter sporshok songkranto upopadyo (Chapter 15)
এই পর্বে রইল দশম শ্রেণির বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য অধ্যায়ের কষে দেখি 15.1 ও 15.2 থেকে কয়েকটি গুরুত্বপূর্ণ গাণিতিক সমস্যার আলোচনা।
[কষে দেখি 15.1]
1. মাসুম O কেন্দ্রীয় একটি বৃত্ত অঙ্কন করেছে যার AB একটি জ্যা। B বিন্দুতে একটি স্পর্শক অঙ্কন করেছে যা বর্ধিত AO কে T বিন্দুতে ছেদ করল। ∠BAT = 21° হলে, ∠BTA এর মান কত হবে?
সমাধান-
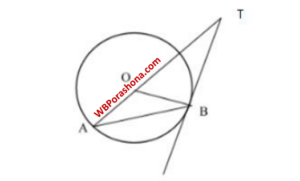
O কেন্দ্রীয় বৃত্তের AB একটি জ্যা, B বিন্দুতে স্পর্শক বর্ধিত AO কে, T বিন্দুতে ছেদ করেছে এবং ∠BAT = 21°
এখানে, OB ⊥ BT সুতরাং, ∠OBT = 90°
△OAB এর, OA = OB [ একই বৃত্তের ব্যাসার্ধ ]
∠BAO = ∠ OBA = 21°
[ ∠BAT = ∠BAO = 21°]
আবার, △ABT এর ∠BAT = 21°
∠ABT = ∠OBT + ∠OBA = 90° + 21°
= 111°
এবং ∠BTA = 180° -(∠ABT + ∠TAB)
=180° – (111° +21°)
=180° – 132°
=48°
উত্তর – নির্ণেয় ∠BTA =48°.
মাধ্যমিকে নম্বর বাড়াবার সেরা উপায় ↓
2. কোন বৃত্তের XY একটি ব্যাস। বৃত্তটির উপর অবস্থিত A বিন্দুতে PAQ বৃত্তের স্পর্শক। X বিন্দু থেকে বৃত্তের স্পর্শকের উপর অঙ্কিত লম্ব PAQ কে Z বিন্দুতে ছেদ করেছে। প্রমাণ কর যে, XA, YXZ এর সমদ্বিখণ্ডক।
সমাধান-
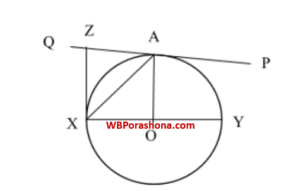
প্রদত্ত- O কেন্দ্রীয় বৃত্তের XY একটি ব্যাস। বৃত্তটির উপর অবস্থিত A বিন্দুতে PAQ বৃত্তের স্পর্শক। X বিন্দু থেকে বৃত্তের স্পর্শকের উপর অঙ্কিত লম্ব PAQ কে Z বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে, XA রেখাটি ∠YXZ এর সমদ্বিখণ্ডক।
অঙ্কন- O, A বিন্দুগুলি যুক্ত করা হল।
প্রমাণ- △XOA এর
OX = OA [একই বৃত্তের ব্যাসার্ধ ]
∠OXA = ∠OAX [ সমদ্বিবাহু ত্রিভুজের কোণ দুটি সমান ]
OA ⊥ PQ [ OA বৃত্তের ব্যাসার্ধ এবং PQ স্পর্শক ]
সুতরাং, ∠OAP = 90°
আবার প্রদত্ত ∠XZA = 90°
সুতরাং, ∠XZA = ∠OAP = 90° [ কোণ দুটির অনুরুপ বাহুগুলি সমান্তরাল হবে]
অতএব, OA ∥ XZ
OA ∥ XZ, AX ভেদক
∠OAX = ∠AXZ [একান্তর কোণ]
∠OXA = ∠AXZ [ ∠OAX = ∠OXA]
XA , ∠YXZ এর সমদ্বিখণ্ডক। [প্রমাণিত]
[কষে দেখি 15.2]
আরো পড়ো → পথের দাবী গল্পের প্রশ্ন উত্তর
3. 16 সেমি দৈর্ঘ্যের ব্যাসবিশিষ্ট একটি বৃত্তের কেন্দ্র থেকে 17 সেমি দূরত্বে অবস্থিত বহিঃস্থ একটি বিন্দু থেকে অঙ্কিত বৃত্তের স্পর্শকের দৈর্ঘ্য কত হবে?
সমাধান-
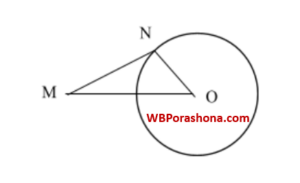
ধরি O কেন্দ্রীয় বৃত্তের কেন্দ্র O থেকে M বিন্দুর দূরত্ব (OM) 17 সেমি এবং ব্যাসার্ধ (ON) = $\frac{16}{2}=8$ সেমি।
সমকোণী △OMN এর,
লম্ব2+ভুমি2=অতিভুজ2
[পিথাগোরাসের উপপাদ্য থেকে পাই ]
বা, \(MN^2+ON^2=OM^2\)
বা, \(MN^2+8^2=17^2\)
বা, \(MN^2=289-64\)
বা, \(MN^2=225\)
বা, \(MN=15\)
উত্তর – M বিন্দু থেকে স্পর্শকের দৈর্ঘ্য MN = 15 সেমি।
পড়া মনে রাখার সেরা উপায়! ↓
4. একটি বৃত্তের উপর অবস্থিত P ও Q বিন্দু দুটিতে অঙ্কিত স্পর্শক দুটি A বিন্দুতে ছেদ করেছে। ∠PAQ = 60° হলে ∠APQ এর মান কত হবে?
সমাধান-
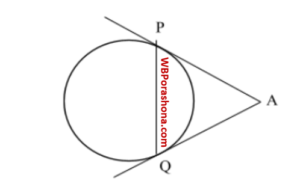
বৃত্তের উপর অবস্থিত P ও Q বিন্দু দুটিতে অঙ্কিত স্পর্শক AP ও AQ দুটি A বিন্দুতে ছেদ করেছে।
আমরা জানি, বহিঃস্থ কোন বিন্দু থেকে বৃত্তের উপর অঙ্কিত স্পর্শক দুটির দৈর্ঘ্য সবসময় সমান হয়।
AP = AQ
△APQ এর, AP = AQ
∠APQ = ∠AQP [ যেহেতু সমদ্বিবাহু ত্রিভুজের দুটি কোণ সমান]
∠APQ = ∠AQP = \(\frac{180^{\circ}-\angle PAQ}{2}\)
\(=\frac{180^{\circ}-60^{\circ}}{2}\)
\(=\frac{120^{\circ}}{2}\)
=60°
∠APQ = 60°
উত্তর – নির্ণেয় ∠APQ এর মান 60°।
আরো পড়ো → অংশীদারি কারবার অধ্যায়ের কিছু গাণিতিক সমাধান
WBPorashona.com-এর পোস্ট আপডেট নিয়মিত পাওয়ার জন্য –
- ফলো করো → WhatsApp চ্যানেল
- সাবস্ক্রাইব করো → YouTube চ্যানেল
- লাইক করো → Facebook পেইজ
- সাবস্ক্রাইব করো → টেলিগ্রাম চ্যানেল
আমাদের কাজ থেকে উপকৃত হলে এই লেখাটি বন্ধুদের সাথে শেয়ার করার অনুরোধ রইল।




