
শ্রেণি – দশম | বিভাগ – গণিত | অধ্যায় -ত্রিকোণমিতিক অনুপাতের প্রয়োগঃ উচ্চতা ও দূরত্ব (Trikonmitik Onupater Proyog Uccota ebong Durotwo) | Height and Distance (Chapter 25)
এই পর্বে রইল দশম শ্রেণির ত্রিকোণমিতিক অনুপাতের প্রয়োগঃ উচ্চতা ও দূরত্ব অধ্যায়ের কষে দেখি 25 থেকে কয়েকটি গুরুত্বপূর্ণ গাণিতিক সমস্যার আলোচনা।
1। 150 মিটার লম্বা সুতো দিয়ে একটি মাঠ থেকে ঘুড়ি ওড়ানো হয়েছে। ঘুড়িটি যদি অনুভূমিক রেখার সাথে \(60^{\circ}\) কোণ করে উড়তে থাকে, তাহলে ঘুড়িটি মাঠ থেকে কত উঁচুতে রয়েছে?
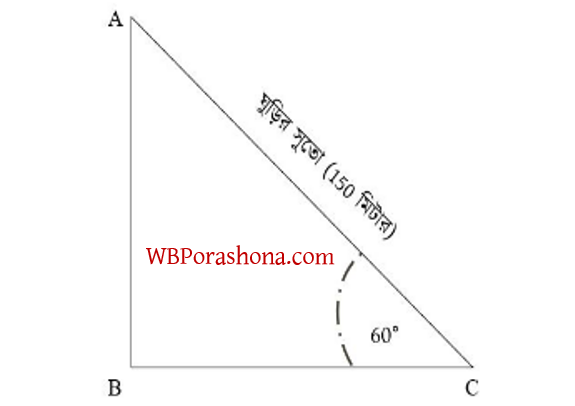
সমাধান- \(AC\) সুতোর দৈর্ঘ্য 150 মিটার
ভূমি (\(BC\)) এর সাথে ঘুড়িটির উন্নতি কোণ ∠ACB = \(60^{\circ}\)
AB = মাঠ থেকে ঘুড়িটির উচ্চতা
△ABC থেকে পাই,
sinθ = লম্ব\ অতিভুজ
বা, \(sin60^{\circ}=\frac{AB}{AC}\)
বা, \(\frac{\sqrt3}{2}=\frac{AB}{150}\)
বা, \(AB = \frac{150\times\sqrt3}{2}\)
বা, \(AB=75\sqrt3\)
সুতরাং, ঘুড়িটি মাঠ থেকে \(75\sqrt3\) মিটার উঁচুতে রয়েছে।(উত্তর)
আরো পড়ো → পরিবেশ দূষণ অধ্যায়ের প্রশ্ন ও উত্তর
2। একটি চিমনির সঙ্গে একই সমতলে অবস্থিত অনুভূমিক সরলরেখায় কোনো এক বিন্দু থেকে চিমনির দিকে 50 মিটার এগিয়ে যাওয়ায় তার চূড়ার উন্নতি কোণ \(30^{\circ}\) থেকে \(60^{\circ}\) হল। চিমনির উচ্চতা কত?

সমাধান- ধরি, AB হল একটি চিমনি
C বিন্দুতে উন্নতি কোণ \(\angle ACB = 30^{\circ}\)
D বিন্দুতে উন্নতি কোণ \(\angle ADB = 60^{\circ}\)
CD = 50 মিটার
আবার, BC = BD + CD = BD + 50 ….(i)
তাহলে △ABD থেকে পাই,
tanθ = লম্ব\ ভূমি
বা, \(tan60^{\circ}=\frac{AB}{BD}\)
বা, \(\sqrt3=\frac{AB}{BD}\)
বা, \(AB=\sqrt3 BD\) ….(ii)
আবার △ABC থেকে পাই,
বা, \(tan30^{\circ}=\frac{AB}{BC}\)
বা, \(\frac{1}{\sqrt3}=\frac{\sqrt3 BD}{BD+50}\) [(i) ও (ii) নং সমীকরণে থেকে পাই ]
বা, \(\sqrt3 \times \sqrt3 BD =BD+50\)
বা, \(3BD -BD=50\)
বা, \(2BD=50\)
বা, \(BD=25\)
(ii) নং সমীকরণে $BD$ এর মান বসিয়ে পাই,
\(AB = \sqrt3 BD=25\sqrt3\)
সুতরাং, চিমনির উচ্চতা \(25\sqrt3\) মিটার। (উত্তর)
আরো পড়ো → তাপের ঘটনাসমূহ অধ্যায়ের প্রশ্ন ও উত্তর
3। উড়োজাহাজের একজন যাত্রী কোন একসময় তার এক পাশে হাওড়া স্টেশনটি এবং তার বিপরীত পাশে শহিদ মিনারটি যথাক্রমে \(60^{\circ}\) ও \(30^{\circ}\) অবনতি কোণে দেখতে পান। ওই সময়ে উড়োজাহাজটি যদি \(545\sqrt3\) মিটার উঁচুতে থাকে, তাহলে হাওড়া স্টেশন ও শহিদ মিনারের দূরত্ব কত?
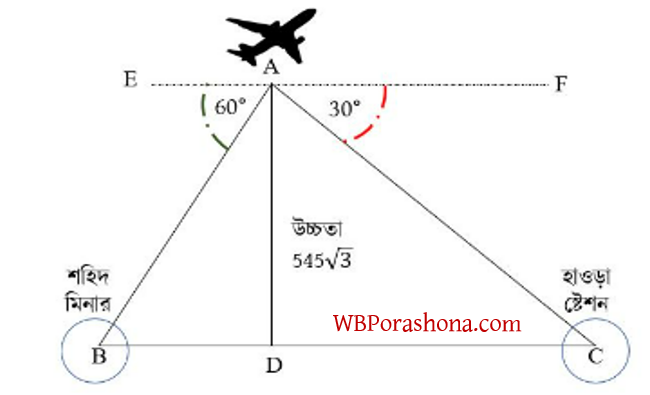
সমাধান- ধরি, A, B ও C বিন্দু তিনটি যথাক্রমে উড়োজাহাজ, শহিদ মিনার ও হাওড়া স্টেশন কে চিহ্নিত করছে।
AD হল উড়োজাহাজের উচ্চতা \(AD = 545\sqrt3\) মিটার
অবনতি কোণ ∠EAB = \(60^{\circ}\) এবং \(∠FAC = 30^{\circ}\)
ধরি, BC ∥ EF
সুতরাং, \(\angle EAB = \angle ABD = 60^{\circ}\) [ একান্তর কোণ ]
এবং \(\angle FAC = \angle ACD = 30^{\circ}\) [ একান্তর কোণ ]
তাহলে △ABD থেকে পাই,
tanθ = লম্ব\ভূমি
বা, \(tan60^{\circ}=\frac{AD}{BD}\)
বা, \(\sqrt3=\frac{545\sqrt3}{BD}\)
বা, \(BD=\frac{545\sqrt3}{\sqrt3}\)
বা, \(BD=545\)
আবার △ADC থেকে পাই,
tanθ = লম্ব\ ভূমি
বা, \(tan30^{\circ}=\frac{AD}{DC}\)
বা, \(\frac{1}{\sqrt3}=\frac{545\sqrt3}{DC}\)
বা, \(DC = 545\sqrt3 \times \sqrt3\)
বা, \(DC = 545 \times 3\)
বা, \(DC = 1635\)
\(BC = BD + DC =545 + 1635 = 2180\)
সুতরাং, হাওড়া স্টেশন ও শহিদ মিনারের দূরত্ব 2180 মিটার। (উত্তর)
আরো পড়ো → প্রলয়োল্লাস অধ্যায়ের প্রশ্ন ও উত্তর
4। মাঠের মাঝখানে দাঁড়িয়ে মোহিত একটি উড়ন্ত পাখিকে প্রথমে উত্তরদিকে \(30^{\circ}\) উন্নতি কোণে এবং 2 মিনিট পরে দক্ষিণ দিকে \(60^{\circ}\) উন্নতি কোণে দেখতে পেল। পাখিটি যদি একই সরল রেখা বরাবর \(50\sqrt3\) মিটার উঁচুতে উরে থাকে, তবে তার গতিবেগ কিলোমিটার প্রতি ঘণ্টায় কত?

সমাধান- ধরি, মোহিত A বিন্দুতে দাঁড়িয়ে উড়ন্ত পাখিটিকে প্রথমে উত্তর দিকে দেখল B বিন্দুতে এবং 2 মিনিট পর দক্ষিণ দিকে দেখল C বিন্দুতে।
পাখিটি \(AD = 50\sqrt3\) মিটার উচ্চতায় রয়েছে।
উত্তরের উন্নতি কোণ ∠BAP = \(30^{\circ}\)
দক্ষিণের উন্নতি কোণ ∠CAQ = \(60^{\circ}\)
∠ABD = ∠BAP = \(30^{\circ}\) [একান্তর কোণ ]
আবার, ∠ACD = ∠CAQ = \(60^{\circ}\) [একান্তর কোণ ]
△ABD থেকে পাই,
tanθ = লম্ব\ ভূমি
বা, \(tan30^{\circ}=\frac{AD}{BD}\)
বা, \(\frac{1}{\sqrt3}=\frac{50\sqrt3}{BD}\)
বা, \(BD=50\sqrt3 \times \sqrt3\)
বা, \(BD = 50\times 3\)
বা, \(BD=150\)
আবার, △ACD থেকে পাই,
\(tan60^{\circ}=\frac{AD}{CD}\)
বা, \(\sqrt3=\frac{50\sqrt3}{CD}\)
বা, \(CD=\frac{50\sqrt3}{\sqrt3}\)
বা, \(CD=50\)
সুতরাং, \(BC = BD + CD =(150 + 50) =200\)
অর্থাৎ পাখিটি 2 মিনিটে যায় 200 মিটার
পাখিটি 1 মিনিটে যায় \(\frac{200}{2}\) মিটার
পাখিটি 60 মিনিটে যায় \(\frac{200\times 60}{2}=6000\) মিটার
সুতরাং, পাখিটির গতিবেগ 6 কিমি/ঘণ্টা। (উত্তর)
আরো পড়ো → পিথাগোরাসের উপপাদ্য অধ্যায়ের কিছু গাণিতিক সমাধান
WBPorashona.com-এর পোস্ট আপডেট নিয়মিত পাবার জন্য –
- সাবস্ক্রাইব করো → YouTube চ্যানেল
- লাইক করো → Facebook পেইজ
- সাবস্ক্রাইব করো → টেলিগ্রাম চ্যানেল
আমাদের কাজ থেকে উপকৃত হলে এই লেখাটি বন্ধুদের সাথে শেয়ার করার অনুরোধ রইল।


